Von den Fraktalen bin ich nicht so überzeugt. Sie helfen ein wenig Ordnung in das Chaos zu bringen und vielleicht beschreiben sie, wie ein einziges spezielles System funktioniert und erzeugen definitiv spannende Bilder. Aber ich sehe nicht, wie man daraus eine allgemeine Theorie bilden kann. Das Problem ist ja, dass jedes System sein eigenes Chaos hat, dass natürlich interessant ist zu untersuchen, aber diese Bifurcationskarte sieht für jedes System eben komplett anders aus. Zumal du ja für jedes System ersteinmal die Observablen neu finden und benennen musst um sie in so eine Karte eintragen zu können.
Was mich aber am meisten stört ist, dass ich nicht sagen kann, ob diese Fraktale wirklich intrinsisch in den Zahlen stecken oder ob diese Bilder nicht auch einfach auf die Rechenfehler unserer Computeralgebra zurückzuführen sind. Ich werde mal schauen, ob ich Zeit finde um dieses Modell nachzuprogramieren. Mich würde wirklich interessieren, wie sich die Genauigkeit der Fließkommazahlen auf das Endergebnis auswirkt. Die Mandelbrotmenge hab ich damals als Abi-Abschlusspräsentation porgramiert, aber natürlich mit der Standard Java Genauigkeit.
Denn der Chaostheorie nach ist ja die Ursache des Chaos in dem Unterschied der exakten Startbedingungen eines Systems zu finden. Also dass zwei komplett exakte Systeme mit nur einer minimalsten Abweichung von nur einer Variable nach einer gewissen Evolutionszeit des Systems zu so großen Abweichungen führt, dann man denkt zwei komplett unterschiedliche Systeme zu betrachten obwohl man quasi mit dem selben Werten gestartet ist, also z.B. nur eine Abweichung von 99.{beliebig aber endlich viele 9}%. Das Problem dabei ist aber, dass wir jede Simulation immer nur mit einer endlichen Genauigkeit berechnen können und somit gibt es immer Abweichungen (Unschärfe) in den Rechenschritten, selbst die Zeit unterliegt diesem Problem als Rechenschritt.
Was physikalisch dabei ja passiert ist, dass jeder Variable bei jedem Rechenschritt mit dem Fehlerfortpflanzungsgesetz einen größeren Fehler zugeschrieben werden muss und der Fehler eines Computers ist eben immer wenigstens seine Gleitkommazahldarstellung. Wenn man die chaotischen Systeme also mitsamt so einer Fehlerbetrachtung durchrechnet, dann stellt man fest, dass alle Fehler mit der Rechenzeit exponentiell ansteigen. Es gibt also zwangsweise relativ schnell irgendwann einen Zeitpunkt, an dem ist wegen der Rechenfehler einfach keine weitere Aussage über das System möglich. Was ein Physiker also eigentlich in der Simulation machen müsste ist irgendwann zu sagen: Die Fehler der Simulation sind so groß, dass wir keine Aussagen mehr über das System treffen können und er müsste die Fehlerbalken angeben.
Die Frage ist also: sind diese Fraktale wirklich schon in den Zahlen und Gleichungen vorgegeben, die wir mit N aus 1+1=2 definieren und zu R oder C logisch erweitern können oder sind die Fraktale nur Artefakte unserer endlichen Rechengenauigkeit, also dass wir jede Simulation durch Rundungsfehler verfälschen?
Aber unabhängig davon bleibt die Erkenntnis, dass solche Simulationen eben immer Fehlerbehaftet sein werden, solange wir herkömmliche Computer verwenden. Quantencomputer könnten aber vielleicht genauere Ergebnisse liefern weil die einzelnen Rechenschritte ja dann nicht mehr gerundet werden sondern wahrscheinlich nurnoch (oder größtenteils) das Endergebnis beim Auslesen digitalisiert (gerundet) wird. Aber auch da könnten sich Rechenfehler durch z.B. keine perfekte Verschränkung einschleichen.
Und um nocheinmal über die Selektionskarte zu reden: physikalsich gibt es ja in der newtonschen Mechanik das Konzept des Phasenraumes: Alle Objekte im System werden in einen 2N-Dimensionalen Vektorraum gesteckt: 3 Ortsvariablen und 3 Geschwindigkeitsvariablen für 3 Dimensionen. Dieser Vektorraum enthält also in seiner Erweiterung auf R alle möglichen Zustände, die das System irgendwie annehmen könnte (ob es das in der zeit tut oder nicht) und jede Entwicklung in der Zeit ändert nur den Ort im Phasenraum, wo sich das aktuelle System gerade befindet.
Auch aus dem Phasenraum kann man lustige Dinge ableiten, z.B. das es unendlich viele gleichwertige Phasenräume für ein System gibt weil ja die Ortsvariablen mathematisch transformiert werden können. Für das System macht es z.B. keinen Unterschied, ob der Ort in Kugelkoordinaten oder kartesischen Koordinaten vorliegt, der Phasenraum sieht dann aber mit den anderen Koordinaten auch anders aus. Solche äquivalente Transformationen gibt es zuhauf in der Physik oder anders gesagt: Die Physik besteht fast nur aus solchen Transformationen und es eine Aufgabe der Physiker die passenden Transformationen zu finden, die die Beschreibung des Systems nicht ändert aber möglichst anschaulich bzw. einfach beschreiben und rechnen lässt.
Genau deswegen betone ich auch regelmäßig, dass auch Gegenstände den gleichen Gesetzmäßigkeiten unterliegen.
Mein Problem in der Wortfindung ist, dass ich zwei verschiedene Begriffe der Macht habe, aber nocheinmal einen Schritt zurück:
Modelltheorie: Jedes vorstellbare System kann man sich grundlegend immer so vorstellen, dass man mit einem komplett leerem System anfängt und darin Objekte platziert. Man definiert sich also z.B. einen Boden und gibt ihm die Fähigkeit andere Dinge anzuziehen. Dann definiert man sich z.B. einen Ball. Ganz einfaches System mit nur 2 Objekten, die miteinander interagieren. Dann lässt man die Zeit loslaufen und schaut, was so im System passiert: der Ball fällt mit zunehmender Geschwindigkeit runter.
Was die Physiker jetzt machen ist sich eine Energie zu definieren um daraus einfach ableiten zu können wie schnell der Ball auf den Boden aufkommt: Potentielle Energie wird durch die Wirkung des Bodens in kinetische Energie umgewandelt…
Dann könnten wir uns jetzt noch das Objekt Luft dazu definieren, die somit den Fall abbremst. Und beliebig weitere Objekte, die die Betrachtung eben immer weiter verkomplizieren.
Was wäre aber, wenn ich gesagt hätte dass der Boden nicht nach unten zieht sondern vielleicht nach rechts ablenkt? Dann würde der Ball nicht nach unten fallen sondern oben an seiner Startposition Kreise drehen. Das wäre die Erklärung für Magnetismus, aber wenn wir so die Erde beschreiben wollen würden wäre dieses Modell eben falsch.
Worauf ich hinaus will ist, dass Modelle eben immer von der Realität abweichen und es somit (wenn auch geringe) Fehler im System gibt. Alleine das Platzieren der Objekte im System, was wir oben beim Chaos gesehen haben, kann schon Fehler in das System bringen, die wir beachten müssen.
Und jetzt kommen erst die Menschen ins Spiel: Jeder Mensch erstellt sich aufgrund seiner Erfahrungen und seines Wissensstandes jederzeit ein Modell seiner Umgebung: sein Weltbild. Und aus diesem Weltbild leitet der Mensch dann jederzeit seine Entscheidungen ab. Beispiel Morgenritual: Ein Mensch kennt seine Wohnung und weiß wo jedes Objekt ist, das er braucht, er geht auf Klo ins Bad, in die Küche zum Essen usw. Auch wenn der Mensch nicht genau darüber nachdenkt hat er ein Modell der Wohnung in seinem Kopf und plant seine Zeit so, dass er möglichst effizient alle nötigen Dinge zum Leben abarbeitet: Essen, schlafen, Spielen usw. Aber wie gut er dabei ist hängt eben davon ab, wie gut sein Modell im Kopf ist, also wie übereinstimmend sein Modell mit der Wirklichkeit ist. Wenn z.B: das Müsli alle ist, er aber denkt er hätte noch welches, dann gibt es einen offensichtlichen Konflikt vom Modell zur Realität. Wen der Mensch sich den Fuß an der Sofakante stößt, dann stand das Sofa oder der Fuß nicht genau dort, wo er es erwartet hat, das Modell im Kopf war fehlerhaft.
Genau deswegen muss das Modell im Kopf jederzeit mit den eigenen Sinnesorganen abgeglichen werden: Augen, Tastsinn, Schmerz usw. Das ist der Realitätscheck.
Und darauf kommt dann das Evolutionsprinzip: Die Menschen mit den besten Modellen oder das beste Weltbild, also die die Welt so realistisch wie möglich im Kopf haben, die haben Vorteile im Leben. Aber ich habe bis jetzt von Menschen geredet: das gilt natürlich auch für Tiere oder Pflanzen. Eine Pflanze, die nur nach unten wächst hat eben keine große Überlebenschance ohne Licht usw. Deswegen Erweitere ich diese Modelltheorie auf alle Objekte: Jedes Objekt könnte sich theoretisch ein eigenes Modell der Umwelt schaffen, eine Pflanze sieht die Umwelt deutlicher als ein Stein, der nur seine Oberfläche hat um interagieren zu können. Und ein Mensch mit Augen sieht wieder mehr als eine Pflanze.
Der große Unterschied zwischen lebender Materie und Toter Materie ist lediglich, dass lebende Objekte auf Umwelteinflüsse mithilfe der physikalischen Schranken reagieren können und versuchen sich mithilfe ihres Modelles oder Weltbildes so gut wie möglich zu entscheiden und damit vorrausplanen. Tote Materie kann sich nur entlang der physikalischen Schranken (Zwangsbedingungen) bewegen. Tote Materie interagiert also auch, sucht sich aber von den vielen möglichen Handlungsmöglichkeiten keine aus sondern reagiert nur auf Interaktionen im physikalischem Sinne. Das ist der evolutionäre Vorteil von lebender Materie.
Der Mittelpunkt der Welt ist für mich die Modelltheorie, quasi als Metatheorie in die man jede andere Theorie einbetten kann, die man sich ausdenken kann. Beginnend mit einfachen Axiomen:
- Jedes System besteht aus beliebig vielen Objekten oder auch Akteure genannt, die alle jederzeit miteinander wechselwirken können.
- Diese Wechselwirkungen werden über die Fähigkeiten der Objekte/Akteure definiert.
- Jeder Akteur kann immer als Zusammenschluss mehrerer (oder im Extremfall auch nur ein einzelner) kleiner Objekte/Akteure aufgefasst werden. Sowohl alle mikroskopischen Objekte als auch der Zusammenschluss als makroskopisches Objekt kann mit allen anderen Akteuren über ihre Fähigkeiten wechselwirken. Insbesondere auch die mikroskopischen Akteure wechselwirken mit dem makroskopischem Objekt und definieren so im Zusammenspiel die Fähigkeiten des makroskopischem Objektes. Jeder Akteur ist somit auch immer ein mikroskopischer Teil eines makroskopischem Objektes, auch wenn das nach oben nur das Modell/System oder der Ersteller/Denker des Modells ist. Mit anderen Worten: Man kann jedes System unendlich oft in kleinere Teile zerlegen oder zu einer größeren Gesamtheit zusammensetzen.
- Jedem Akteur kann ein exakter Machtwert zugeordnet werden (quasi die Energie des Akteurs), die er in seiner Struktur (mikroskopische Objekte) speichert. Geht dem makroskopischem Objekt diese Macht aus, dann kann er seine innere Struktur nicht mehr aufrecht erhalten. Der makroskopische Akteur stribt also ab und zersetzt sich in seine Einzelteile.
- Jede Interaktion zwischen Akteuren ist eine Anwendung ihrer Fähigkeiten und sorgt dafür, dass die Machtwerte zwischen den Akteuren ausgetauscht werden. Das Anwenden einer Fähigkeit kostet also immer Macht und senkt den Vorrat der Macht vom anwendenden Akteur ab. Macht ist also ein Maß dafür, wie Einflussreich, Durchdringend oder Weitreichend eine Fähigkeit angewendet werden kann. Ohne ausreichend Macht kann ein Akteur seine Fähigkeiten nicht mehr einsetzen.
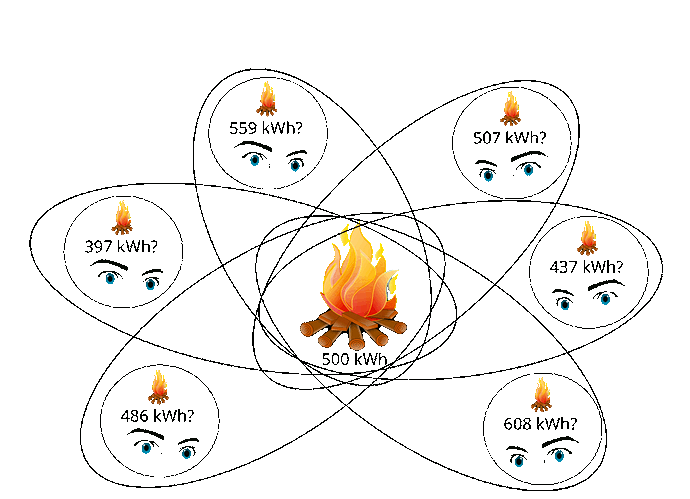
Ich formuliere diese Gesetzmäßigkeiten mit Absicht nicht physikalisch weil sie explizit auch auf unphysikalische Modelle wie Computerspiele oder der Gesellschaft angewendet werden können. Aber jedes Modell, auch Geschichten in Büchern mit z.B. Magie/Esoterik kann man nun analysieren und sich so ein System erstellen indem man objektifiziert: Was sind die handelnden Objekte in dem System und wie interagieren sie miteinander: die Akteure. Vorallem: Wie tauschen sie ihre Macht aus und wohin wandert die Macht mit der Zeit, also wo sammelt sie sich und wo geht sie weg? Wenn ein Magier einen Feuerball aus dem Nichts erstellen kann, dann hat er quasi Macht aus dem Nichts erstellt und somit gegen die physikalische Energieerhaltung verstoßen. Es macht also keinen wirklichen Sinn hier von einem physikalischem System zu sprechen und deswegen auch nicht die physikalische Energie als Beschreibungsparameter zu verwenden. Aber es ist ein valides vorstellbares Modell und wird in vielen Fantasieromanen oder Computerspielen so vermittelt. Dann muss man eben damit leben, dass der Magier eine mehr oder wenig unendliche „Energiequelle“ in seinem System hat aber daran kann man auch erkennen, dass es kein physikalisches System sein kann weil es der Energieerhaltung widerspricht. Es ist trotzdem ersteinmal ein valides Modell für die Bücher oder Spiele und die Aktuere in diesem System müssen mit diesen „neuen physikalischen Gesetzen leben“ oder untergehen. Auch hier gibt es trotzdem ein Selektionsprinzip.
Wenn man jetzt also den Axiomen noch physikalische Regeln hinzufügt wie z.B. eine Machterhaltung kann man sich der Realität weiter Annähern und unphysikalische, also unrealistische Modelle aussieben. Aber egal wie das Modell am ende aussieht, wenn es die Realität möglichst gut abbildet, dann hat derjenige, der so ein gutes Modell verwendet eben Vorteile im Leben als jemand, der schlechtere Modelle verwendet, die eine größere Abweichung von der Realität haben (Selektionsprinzip).
Der Vorteil, dass man jedes Objekt in makroskopsiche und mikroskopische Akteure unterteilt ist, dass man sehr viel Komplexität eines Systems in eine Blackbox stecken kann. Für viele Betrachtungen ist es nicht wichtig, wie die mikroskopischen Zustände genau sind sondern nur das Zusammenspiel aller dieser Objekte ist relevant.
Wen du z.B. einen Baum siehst, dann ist es völlig egal, wie viele Blätter er hat und wie diese aufgebaut sind. Wenn du nur da stehst musst du nicht wissen, dass der Wind durch die Blätter weht und dies somit aneinander reiben und laute von sich geben, die sich zu einem Rauschen verbinden. Es reicht völlig aus zu wissen, dass der Baum durch den Wind raschelt. Relevant wird es erst, wenn du zum Baum gehst und z.B. im Herbst die unterschiedlichen Blattfarben untersuchst. Aber wenn du nur mit dem Auto vorbeifährst ist dieser Baum herzlich irrelevant, er ist nur ein Hindernis wie andere Bäume oder Zäune auch wo man nicht gegenfahren sollte. Dabei ist es völlig egal ob der Baum grün war oder überhaupt keine Blätter mehr hatte.
Diese Betrachtungsweise ermöglicht also beliebig alle Objekte als eine Art Blackbox anzusehen, deren Eigenschaften wir in einem Modell definieren. Diese Definitionen können wir durch Betrachtung der mikroskopischen Ebenen auch begründen bzw. beweisen aber für viele Fälle reicht es einfach aus zu wissen, wie sich dieses Objekt in einem System verhält ohne die mikroskopischen Ebenen mit einbeziehen zu müssen und das macht das System deutlich einfacher, man muss aber darauf achten, dass man die Fähigkeiten und Objekte im System ausreichend genau genug beschreibt.
Für jedes Modell ist es also sinnvoll zu wissen, wo es Gültigkeit hat und wo man es nicht anwenden sollte weil die Abweichungen zur Realität zu groß werden. Und genau das ist ein Teil des evolutionären Prozessen: die Akteure mit einem besseren Modellverständnis setzen sich tendenziell besser durch. Und dabei spielt es keine Rolle, ob sie das bewusst gemacht haben oder ob ein Stein einfach nur „glück“ gehabt hat. Man könnte es auch so formulieren: Wenn Glück zur Gewohnheit wird, dann nennt man es Fähigkeit. Gerade weil man ja dann erkennt, dass in all den zufälligen Prozessen, die auftreten können, eine Positivselektion stattfindet.
Diese Positivselektion kannst du dann versuchen mit Entropie zu beschreiben, denn diese Positivselektion gibt dem Glück ja eine Richtung. Gerade für Menschen hat die Evolution dieses Glück mit dem Zufall der Nerven im Kopf perfektioniert und mit AI können wir zeigen, dass es eben kein einfacher Zufall ist, der für die Gedanken im Kopf sorgt auch wenn die einzelnen Akteure im Kopf, die Nervenzellen, auf dem ersten Blick wahllos ihre Impulse chaotisch feuern.
Mit dieser Vorrede zurück zum Begriff Macht: Das Problem für jedes System ist, dass wir zwar einem Objekt oder Akteur mathematisch einen exakten Machtwert bzw. Energiewert zuschreiben können, solange wir der göttliche Systemersteller oder Modelldenker sind und alle Fähigkeiten und Wechselwirkungen selber definiert haben, aber sobald andere diese Modelle betrachten aber genauso die Akteure im Modell selber können diese Information Gegnerell nicht mehr exakt haben. Sie müssen also immer für sich diese Macht der anderen Objekte bzw. Akteure abschätzen und bewerten und das können sie nur über Interaktion mit diesen Objekten mit der Zeit lernen. Auch ein Stein als Objekt lernt, nur eben mit der Lernkurve von wahrscheinlich 0  sodas er wohl immer verhältnismässig gleich auf eine Krafteinwirkung reagieren wird. Ein Mensch würde bei einer gleichen Krafteinwirkung schon deutlich anders reagieren und viele Menschen auf so ein Ereignis komplett unterschiedlich und somit nicht unbedingt vorhersagbar.
sodas er wohl immer verhältnismässig gleich auf eine Krafteinwirkung reagieren wird. Ein Mensch würde bei einer gleichen Krafteinwirkung schon deutlich anders reagieren und viele Menschen auf so ein Ereignis komplett unterschiedlich und somit nicht unbedingt vorhersagbar.
Für jedes Objekt gibt es also immer einen exakten (meist unbekannten) Machtwert, den man mit seinen Erfahrungen oder Weltbild abschätzen muss um zu wissen, wie dieses Objekt reagieren kann. Evolutionär eine wichtige Aufgabe diese Einschätzung weil die Akteure zwischen freundlichen oder tödlichen Ereignissen unterscheiden mussten. Bzw. anders gesagt: Das Selektionsprinzip hat ganz automatisch die tödlichen Entscheidungen ausgesiebt.
Jeder Akteur rechnet für sich also mit einem leicht anderen Machtwert und bewertet diese Macht der anderen Objekte also anders und kommt damit auf ein für sich anderes Weltbild. Genau hier kommt erst die subjektivität ins Spiel, die dafür sorgt, dass der exakte Machtbegriff verwaschen wird, quasi unscharf.
Es gibt also zwei Machtbegriffe, die ich noch irgendwie trennen muss: der exakte Machtwert und der von einem Akteur zugesprochene bzw. subjetiv bewertete Machtwert.
Insgesamt habe bis jetzt aber noch kein besseres Wort für diese generelle Energie gefunden als Macht oder Einfluss. Diese Worte beschreiben einfach treffend, wie eine Fähigkeit generell wirkt, egal ob diese Fähigkeit ausgedacht ist oder in einem realem System existiert.
Das Selektionsprinzip besteht also aus der Beobachtung, dass in jedem beliebigen Modell sich die Macht an den Potentialminimas sammelt und diese Potentiallandschaft gibt die Richtung des Machtflusses vor. Gibt es keine solchen Minimas, dann verteilt sich die Macht gleichmäßig mit der Zeit auf alle Akteure auf weil alle Akteure miteinander wechselwirken und ihre Macht austauschen. In diesem Gleichgewicht bekommen sie also immer genauso viel Macht wie sie abgeben, egal wo sie sich im System befinden. Das ist der Zustand höchster Entropie.
Gleichzeitig kann es auch ein Gefälle an Macht geben, also ein Machtfluss von einer Quelle zu einer Senke. Auch hier kann sich ein Machtgleichgewicht einstellen, nur dass die Akteure an der Quelle eben mehr Macht haben als die Akteure, die weiter weg von der Quelle sind.
Damit erkennt man z.B. sehr leicht die Thermodynamischen parallelen zu einer Gesellschaft, wo es eine Machtquelle gibt wie das Drucken von Geld oder die Religion und die Vorgabe eines Weltbildes. Man kann eben immer jede Gesellschaft in ein Modell stecken indem man die handelnden Objekte dieses Systems benennt und ihre Fähigkeiten und Machtwerte kennt. Wie gut ein spezielles Modell wirklich ist, also eine spezielle Realisierung einer Gesellschaft in so einem Modell kann dann aber nur der Realitätscheck feststellen und trotzdem können wir davon ausgehen, dass die physikalischen Gesetze für alle so definierten Systeme gültig bleiben müssen: Allen voran die Machterhaltung aber auch die Steuerung der Machtflüsse durch Entropie oder Dizzipation.
Einfache Schlussfolgerungen sind also auch in Gesellscahftlichen Systemen Möglich: Wenn es einen König gibt, der entgegen seinen Machverlusten durch Anwendung von Fähigkeiten (oder wegen der Selbstentladung bzw. Dizzipation durch seine Bestandteile) keine Macht verliert, dann muss es Effekte in dem System geben, die dafür sorgen dass er wieder an Macht gewinnt (einfache Folge aus der Machterhaltung). Man kann das System also untersuchen, wo er diese Macht her bekommt. Hat er eine Rohstoffquelle? Dann muss die mit der Zeit zuneige gehen weil die Rohstoffquelle an Macht verliert. Beutet er seine Bevölkerung aus? Dann muss seine Bevölkerung diese Macht verlieren und zusehen, wo sie diese Macht her bekommen, denn zusätzlich zum Eigenverbrauch an Macht müssen sie ja jetzt auch den König mit Macht subventionieren. Es gibt also zwei Möglichkeiten: der König nimmt sich so viel Macht, dass die Bevölkerung insgesamt an Macht verliert und somit langfristig ausstirbt, dann ist damit aber auch die Zeit des Königs gezählt. Oder die Bevölkerung kann sich diese Abgaben leisten und stabil in einem Machtgleichgewicht mit ihrem König leben.
Wenn man sich all diese Objekte anschaut, dann hat der König natürlich eine hohe positives Selektionwahrscheinlichkeit weil er mächtiger ist als alle anderen. In vielen vorstellbaren Krisen hat er somit eine deutlich bessere Überlebenschance als ein einfacher Bauer. Handelt der König dazu noch weise, dann hat das ganze Königreich eine hohe Überlebenschance weil die Menschen dann in dem stabilem Zustand mit ihrem König leben. Ist der König jedoch ein Tyrann, dann vernichtet er seine Lebensgrundlage mit dem Verarmen seiner Bevölkerung selber. Während der Tyrann also auf der kleinen Zeitskala für sich evolutionäre Vorteile hat so ist die Überlebenschance auf der großen Zeitskala geringer als für den gütigen König mit seinem stabilem Königreich.
So und so ähnlich kann man mithilfe der Modelltheorie und der Macht, die sich physikalisch verhalten muss um die Realität in einem Modell abzubilden zu können generelle Aussagen über jedes beliebige soziale System machen, selbst wenn das System nur ausgedacht ist und sogar Magie beinhaltet. Eragon ist da ein schönes Beispiel wo die Magie trotzdem einer Energieerhaltung unterliegt und somit auch sehr gut analysiert werden kann. Wie gut eine Analyse dann aber wirklich ist kann nur der wirkliche Realitätscheck zeigen: Durch die Positivselektion über ausreichend lange Zeiträume.
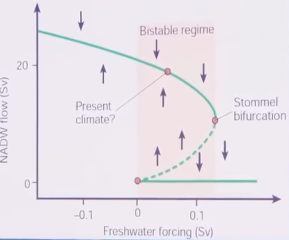
Oder meinst du, dass meine beispielhafte Analyse hier vom Königreich eine Art Bifurcationskarte ist? Überall wo sich Akteure in der Zeit entscheiden können gibt es quasi ein Aufsplitten der Modelle: Ein Modell entwickelt sich so weiter als ob der König gut wäre und ein anderes Modell entwickelt sich so weiter als ob der König ein Tyrann wäre? Das Problem dabei ist, dass jedes Modell in der Mitte ja potentiell auch angenommen werden kann, also z.B. Halbtyrannen oder soziale Psychopathen…
Ich finde die Modelltheorie zumindest absolut spannend, was man damit alles anstellen kann.