Ich schon.
@bit01 Dein Verfahren ist extrem unsicher. Warum?
Weil ich es gerade mit Python gebrochen habe. Alles was ich dafür brauche ist der verschlüsselte Block. Die Permutation innerhalb der Blöcke, die Information welche Blöcke die richtigen sind oder die absichtlich falschen Wörter die versteckt sind bieten keine Sicherheit.
Mir hat diese „Kryptanalyse Lite“ gerade sehr viel Spaß gemacht und hoffe dass man hier was mitnehmen kann. :D
Für alle interessierten die damit rumspielen wollen (und meinen Anfängercode verfeinern möchten), hier könnt ihr das Jupyter Notebook dazu runterladen: https://sutterseba.s-ul.eu/oG2DsjhD
Als Beispiel habe ich einfach das aus dem PDF genommen, unsere Ausgangslage ist also:
Was wir kennen:
-
Das Verfahren
Das ist auch üblich so, ansonsten wäre das ein Verstoß gegen das Kerckhoffs’sche Prinzip. Die Sicherheit einer Chiffre darf auf keinen Fall auf ihrer Geheimhaltung beruhen. Du meintest aber dass das Verfahren trotzdem noch sicher ist, sonst hättest du es ja auch nicht veröffentlicht.
Was wir nicht kennen:
- Den Schlüssel, also
- Die gültigen Blöcke
- Die richtige Reihenfolge der Blöcke
- Absichtlich versteckte Wörter die falsch sind
- Welche Blöcke permutiert wurden und in welche „Richtung“
Los geht’s.
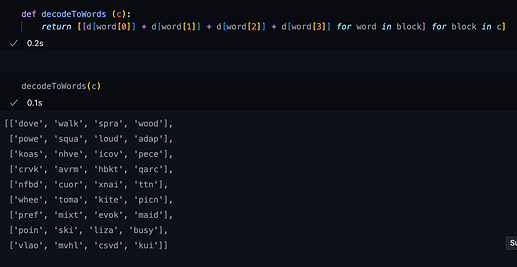
Wir schreiben uns erstmal diesen Zahlensalat in einen halbwegs sinnvollen Datentyp. (Ja, ich weiß, hier hätte ich eigentlich Numpy nutzen sollen…)
Wir sehen hier eine Liste in der jeweils die Blöcke (auch Listen) mit ihren Viererpärchen an Zahlen stehen. Diese Zahlen übersetzen wir jetzt erstmal ins Alphabet:
Einige Wörter machen jetzt bereits Sinn, andere nicht.
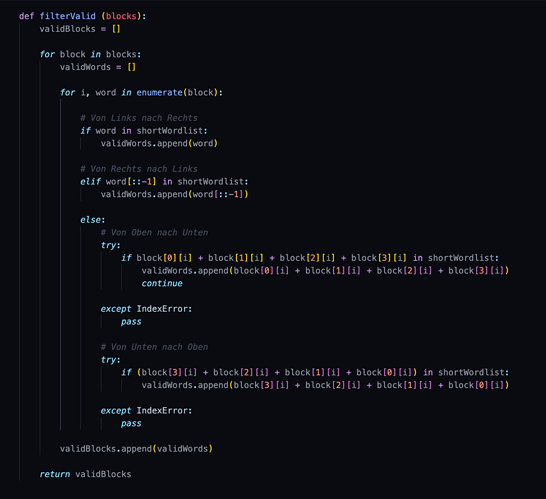
Jetzt permutieren wir alle Wörter die noch keinen Sinn ergeben in alle Richtungen (also von Rechts nach Links, von Oben nach Unten, und so weiter…). Sobald ein Wort einen Sinn ergibt, merken wir es uns, falls alle Richtungen keinen Sinn ergeben, landet das Wort nicht auf der Merkliste. → Brute Force.
Wir bekommen 6 Blöcke mit BIP39 Wörtern, und drei leere Blöcke. Genau was wir haben wollten:
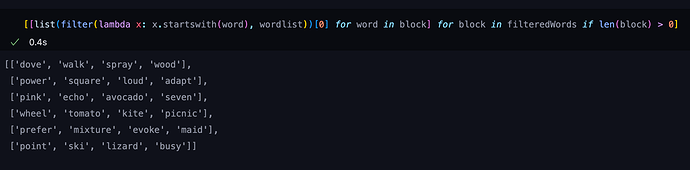
Jetzt schmeißen wir die leeren Blöcke raus und erweitern die Wörter (mit Hilfe der Wordlist) auf ihre eigentliche Länge.
Wir haben jetzt 6 Blöcke die wir nur noch unterschiedlich Permutieren müssen, also in alle möglichen Anordnungen schieben, bis die daraus resultierende Mnemonic gültig ist. Der Suchraum ist hier jediglich 6! = 720, was ein Kinderspiel ist.
Darauf habe ich @bit01 auch schon hingewiesen:
Wir laufen jetzt mit Hilfe von itertools über alle möglichen Anordnungen und überprüfen in jedem Schritt ob die Checksumme und damit die Mnemonic gültig ist. Das hast du, @bit01, wahrscheinlich nicht bedacht.
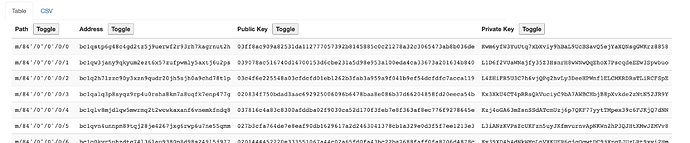
Und heraus bekommen wir eine wunderschöne Mnemonic:
Geld wäre an dieser Stelle (also nach wenigen Mikrosekunden) weg:
\text{q.e.d.}