Bitcoin Gompertz Model

Diskussionen
1

Liebe Community,

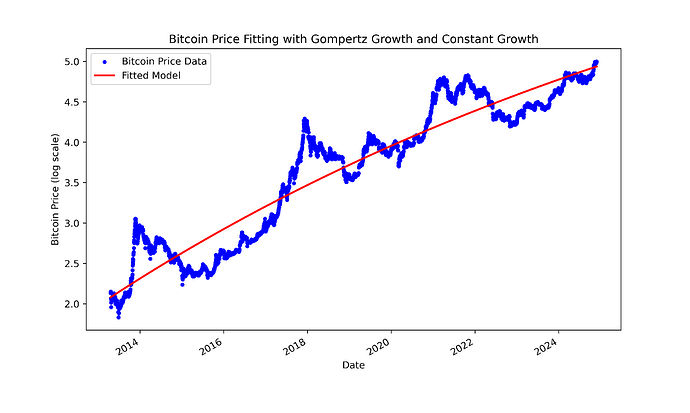
ich arbeite gerade an einem neuen Bitcoin Preis-Modell, was sich in gewisser Weise an dem rainbow chart von Holger orientiert, bzw. dem dahinter liegenden Modell.

Annahmen:
Das Gompertz Modell nimmt an, dass der Bitcoin-Preis mindestens 3 Faktoren hat, die Ihn beeinflussen.

  1. Inflation des Denominators (USD)
  2. Steigende Produktivität
  3. Die Adoptionskurve

(1) und (2) kann man zusammen durch den Anstieg des Weltvermögens zwischen 2009 und jetzt mit etwa 5.8% schätzen. Zu diesem kontinuierlichen Anstieg des Bitcoin-Preises in USD kommt die Adoptionskurve dazu, die wir mit der Gompertz-Funktion modellieren:

Bitcoin-Kurs = 5.8% annualisierte Gewinne * Gewinne durch Adoption

Die 5.8% annualisierten Gewinne sind rasch mit einer Exponentialfunktion modelliert. Die Gompertz-Funktion erfordert neben den Parametern b und c, die wir aus den historischen Kursen schätzen können, auch die „Obergrenze“, die ich als das Weltvermögen in 2009 geteilt durch 21 Millionen („Alles geteilt durch 21 Millionen“) festgelegt habe.

Das Projekt wird auf GitHib gehostet:

Ergebnisse:

Modell-Funktion
a * e^(r * t - b * e^(-c * t))

wobei
a = 10,000,000
r = 0.00015446666
b=15.09837109971362
c=0.00016935349643529076
t = Zeit in Tagen seit 03.01.2009

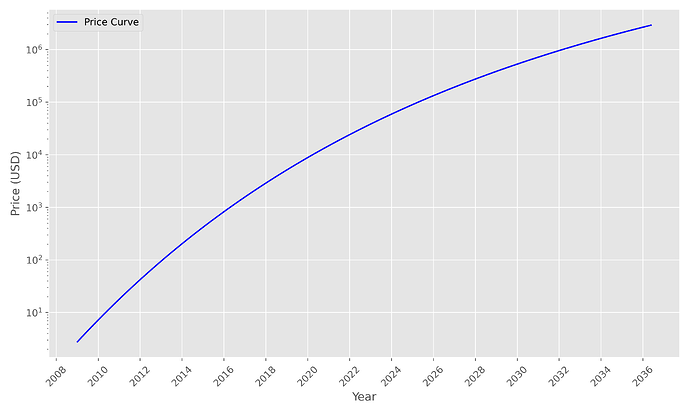
Einblicke und Prognose
Aus der Modellierung von b und c lässt sich schätzen:

  • Bitcoin Adoption aktuell bei 0.357 %
  • 50% Adoption in 2058

Prediction für Top (Annahme: 150 Tage in die Zukunft)

  • Best Case: 323,221 USD
  • Worst Case: 102,008 USD

Bottom für diesen Zyklus (Annahme: 450 Tage in die Zukunft)

  • Best Case: 139,758 USD
  • Worst Case: 42,740 USD

lg,
Jafar

P.S. Keine Finanzberatung! Danke an @foobar für die Diskussion, die das Modell voran gebracht hat. Frühere Versionen hatten andere Schätzwerte, die in der Diskussion auftauchen könnten. Dieser 1. Post spiegelt den aktuellen Stand des Projektes wieder.

4 „Gefällt mir“
2

Interessant, erinnert mich an die Corona-Zeit. :angry:

Bin zur Zeit dem Power-Law Modell recht zugewandt. Für den aktuellen Zyklus passen Deine Predictions ganz gut dazu.

Mich würde mal interessieren, was Dein Modell für die weitere Zukunft vorhersagt: 2034, 2040?

1 „Gefällt mir“
3

Was heisst das genau?

4

12,67% aller Menschen halten Bitcoin

5

Spannende Frage.
Wie misst man „Adoption“?

  • Anhand der Menschen die es nutzen?
  • Anhand der Marktkapitalisierung?
  • andere?

Im o.g. Modell gehen wir davon aus, dass 100% Adoption erreicht ist, wenn das gesamte Weltvermögen in Bitcoin gemessen und ausschließlich in diesem monetären Wert gehandelt wird. 100% Adoption wäre erreicht, wenn Bitcoin sämtliches Kapital aufgesogen hätte:

Bitcoin Black Hole
Bitcoin Black Hole671×475 86.9 KB

Laut Modell ist dieser Prozess zu 12% abgeschlossen. Heißt dass, das 100% die Obergrenze für den Kurs ist? Nein, denn

  • sämtlicher Fortschritt zwischen 2009 und jetzt wird auch aufgesaugt
  • Bitcoin has no Top because Fiat has no bottom.

Jaja, die Gompertz-Funktion wird genutzt um das Ausbreiten von Viren zu modellieren. Bitcoin ist das Pilzgeflecht, was den Planeten überzieht.

1 „Gefällt mir“
6

:face_with_raised_eyebrow:

Wat?

Saylor sagte letztens, er rechnet mit 7% bis 2045, oder so ähnlich.

7

Saylor bezieht sich auf die Relation zum Gesamtvermögen, o.g. Modell bezieht sich auf den Anteil der Marktkapitalisierung, die auf die Adoption zurückzuführen ist. Dieser Adoptions-Anteil wird durch den exponenziellen Teil des globalen Wachstum „verwässert“, sodass der Unterschied gut erklärt werden könnte.

Außerdem: Das Modell kann falsch sein.

edit: Wenn ich das Produkt statt der Summe der Effekte berechne, ist die Adoption aktuell „nur“ 8.14%

01.01.2034: 561,073 USD
01.01.2040: 2,033,487 USD

edit: Wenn ich statt der Summe der Komponente ihr Produkt nehme, sieht es besser aus:
01.01.2034: 915,144
01.01.2034: 5,717,570

Ich überlege noch einmal, ob das Sinn macht, das Produkt zu nehmen. Wenn ja, modelliere ich neu. Insgesamt „gefallen“ mir die Ergebnisse besser, aber es muss ja auch stimmen.

8

Mir auch :wink:

1 „Gefällt mir“
9

So sehe das dann aus:

def model(t, b, c):
      gompertz_term = 1e7 * np.exp(-b * np.exp(-c * (t + 1576)))
      growth_term = np.exp(0.00015446666694824026 * t)
      return gompertz_term * growth_term

b=14.916420963291692
c=0.00017453553049145564

log
log4000×2400 287 KB

Sieht nicht wesentlich anders aus, aber extrapoliert „besser“:

  • Bitcoin Adoption aktuell bei 8.14 %
  • 50% Adoption in 2057

Prediction für Top (Annahme: 150 Tage in die Zukunft)

  • Best Case: 323,221 USD
  • Worst Case: 102,008 USD

Bottom für diesen Zyklus (Annahme: 450 Tage in die Zukunft)

  • Best Case: 139,758 USD
  • Worst Case: 42,740 USD
10

Ich denke Multiplikation der Terme ist korrekt

11

Wie leitest Du denn den Best/Worst Case ab?

12

edit: nach erster Überlegung ist einfaches Produkt vermutlich korrekt.
edit2: Ich denke ich weiß jetzt auch warum. Die Exponential-Funktion modelliert die Obergrenze als „moving target“ der Gompertz-Funktion.

Danke, dass du fragst ;)

Rationale:
Da wir wissen, dass die gesamte Bitcoin-Emission programmatisch vorgegeben und theoretisch zu jedem Zeitpunkt eingepreist sein könnte, können wir daraus ableiten, dass die „überraschenden“ Boom- und Bust-Zyklen nach dem Halving auf Grundlage einer Informationsassymmetrie entstehen, welche mit zunehmender Adoption verschwinden muss.
Daher sollte der „Ausschlag“ nach oben und unten immer kleiner werden. Das sieht man auch in folgender Abbildung:

diff_percent
diff_percent4000×2400 244 KB

Ich habe einfach abgelesen, wie hoch die Abweichung im letzten Zyklus war, und dies als „obergrenze“ festgelegt. Beim Bottom habe ich entsprechend die „Untergrenze“. Das andere Ende des Intervalls ist jeweils der geschätze Kurse, gemäß Modell.

edit: vielleicht geht das auch ezakter, durch hinzunahme der geschätzten Adoption. Sollte sich das Modell als brauchbar erweisen, investiere ich etwas mehr Zeit.

2 „Gefällt mir“
13

Ich habe das Modell und den Code auf GitHub hochgeladen:

Das Modell nutzt das Produkt aus Wachstum und Adoption (siehe Diskussion oben). Der Code ist nicht dokumentiert. Wenn interesse besteht, mache ich das. Außerdem kann ich noch mehr Funktionen implementieren, z.B. eine Funktion, die den Stand der Adoption schätzt. Anbei ein paar ordentliche Abbildungen.

P.S. Beim schätzen der Adoption ist mir zuvor ein Fehler unterlaufen. Der Korrekte wert der aktuellen Adoption ist 0.36 %. Passt das Besser @Shitcoin_Billionaire?

Hier die geschätzte Adoption Curve:

We are indeed still early.

edit: Gerade auf X veröffentlicht:

1 „Gefällt mir“
15

Besser. :+1:

Hast Du den Log Chart auch in die Zukunft, nachdem es ja um diese geht?

1 „Gefällt mir“
16

Klar, kann ich machen…

forecast
forecast4000×2400 168 KB

1 „Gefällt mir“
17

Update: Ich habe endlich eine readme.md geschrieben.

3 „Gefällt mir“
18

das klingt auch irgendwie realistischer als 12%… wobei das immer noch viel ist wie ich finde…
bei 10% ist die kritische masse erreicht…

19

Diese Zahl hat sich durch Update des Modells überholt.

Dass die Adoption ein Ceiling hat, ist interessant. Theoretisch könnte ich das mal so modellieren. Bisher setzt das Modell die Hypothese vorraus „Alles geteilt durch 21 Millionen“. Wenn bei 10% Schluss ist, wäre also „Alles geteilt durch 21 Millionen, mal 10%“

1 „Gefällt mir“